Skip to content

Commit d29ce04

Browse files
EvanLiEvanLi
committed
Edit chap09.
1 parent e84adb2 commit d29ce04

File tree

1 file changed

+286
-7
lines changed

1 file changed

+286
-7
lines changed

‎算法图解/chap09-动态规划.ipynb‎

Lines changed: 286 additions & 7 deletions
Original file line numberDiff line numberDiff line change
@@ -17,7 +17,7 @@
1717
},
1818
{
1919
"cell_type": "code",
20-
"execution_count": 9,
20+
"execution_count": 1,
2121
"metadata": {},
2222
"outputs": [],
2323
"source": [
@@ -66,7 +66,7 @@
6666
},
6767
{
6868
"cell_type": "code",
69-
"execution_count": 11,
69+
"execution_count": 2,
7070
"metadata": {},
7171
"outputs": [
7272
{
@@ -78,7 +78,7 @@
7878
" [0, 1500, 1500, 2000, 3500]]"
7979
]
8080
},
81-
"execution_count": 11,
81+
"execution_count": 2,
8282
"metadata": {},
8383
"output_type": "execute_result"
8484
}
@@ -93,7 +93,7 @@
9393
" if weight[i-1] > W: #当前物品重量大于背包重量，则取i-1个物品时的值\n",
9494
" dp[i][W] = dp[i-1][W]\n",
9595
" else: #当前物品重量小于背包重量，则取两者（不取这个物品、取这个物品）的最大值\n",
96-
" dp[i][W] = max(dp[i-1][W],value[i-1]+dp[i-1][W-weight[i-1]])\n",
96+
" dp[i][W] = max(dp[i-1][W],value[i-1]+dp[i-1][W-weight[i-1]]) #i从1开始，所以是value[i-1],weight[i-1]\n",
9797
" return dp\n",
9898
"\n",
9999
"C = 4 #背包容量\n",
@@ -200,7 +200,7 @@
200200
},
201201
{
202202
"cell_type": "code",
203-
"execution_count": 12,
203+
"execution_count": 3,
204204
"metadata": {},
205205
"outputs": [
206206
{
@@ -214,7 +214,7 @@
214214
" [0, 6, 9, 15, 18, 20, 25]]"
215215
]
216216
},
217-
"execution_count": 12,
217+
"execution_count": 3,
218218
"metadata": {},
219219
"output_type": "execute_result"
220220
}
@@ -226,11 +226,290 @@
226226
"dp = knapsack_dp(value,weight,C)\n",
227227
"dp"
228228
]
229+
},
230+
{
231+
"cell_type": "markdown",
232+
"metadata": {},
233+
"source": [
234+
"## 9.3 最长公共子串(Longest Common Substring)\n",
235+
"\n",
236+
"- 动态规划可帮助你在给定约束条件下找到最优解。在背包问题中，你必须在背包容量给定的情况下，偷到价值最高的商品。\n",
237+
"- 在问题可分解为彼此独立且离散的子问题时，就可使用动态规划来解决。要设计出动态规划解决方案可能很难，这正是本节要介绍的。下面是一些通用的小贴士。\n",
238+
" - 每种动态规划解决方案都涉及网格。\n",
239+
" - 单元格中的值通常就是你要优化的值。在前面的背包问题中，单元格的值为商品的价值。\n",
240+
" - 每个单元格都是一个子问题，因此你应考虑如何将问题分成子问题，这有助于你找出网格的坐标轴。\n",
241+
"\n",
242+
"下面再来看一个例子。假设你管理着网站dictionary.com。用户在该网站输入单词时，你需要给出其定义。\n",
243+
"\n",
244+
"但如果用户拼错了，你必须猜测他原本要输入的是什么单词。\n",
245+
"\n",
246+
"例如，Alex想查单词fish，但不小心输入了hish。在你的字典中，根本就没有这样的单词，但有几个类似的单词。\n",
247+
"\n",
248+
"在这个例子中，只有两个类似的单词，真是太小儿科了。实际上，类似的单词很可能有数千个。\n",
249+
"\n",
250+
"Alex输入了hish，那他原本要输入的是fish还是vista呢？\n",
251+
"\n",
252+
"### 9.3.1 绘制网格\n",
253+
"\n",
254+
"- 单元格中的值是什么？\n",
255+
"- 如何将这个问题划分为子问题？\n",
256+
"- 网格的坐标轴是什么？\n",
257+
"\n",
258+
"网格如下：\n",
259+
"\n",
260+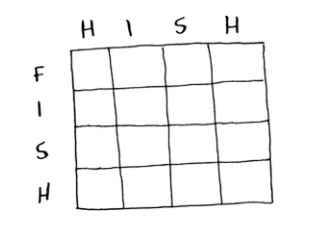
"![](https://raw.githubusercontent.com/hostimg/img/gh-pages/s/20190822192521.png)\n",
261+
"\n",
262+
"### 9.3.2 填充网格\n",
263+
"\n",
264+
"我使用下面的公式来计算每个单元格的值。\n",
265+
"\n",
266+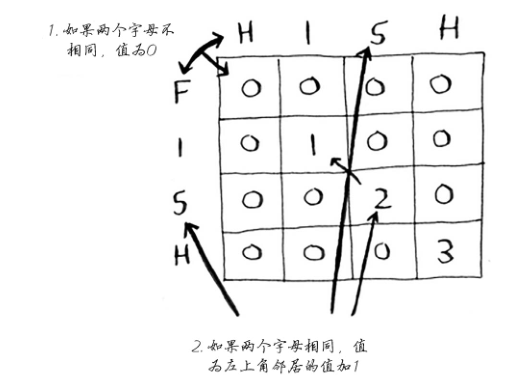
"![](https://raw.githubusercontent.com/hostimg/img/gh-pages/s/20190822192839.png)\n",
267+
"\n",
268+
"实现这个公式的伪代码类似于下面这样。\n",
269+
"```python\n",
270+
"if word_a[i] == word_b[j]: # 两个字母相同\n",
271+
" cell[i][j] = cell[i-1][j-1] + 1\n",
272+
"else: # 两个字母不同\n",
273+
" cell[i][j] = 0\n",
274+
"```\n",
275+
"\n",
276+
"查找单词hish和vista的最长公共子串时，网格如下。\n",
277+
"\n",
278+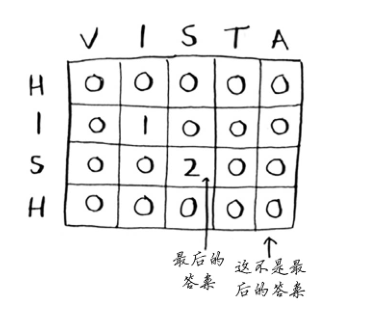
"![](https://raw.githubusercontent.com/hostimg/img/gh-pages/s/20190822193257.png)\n",
279+
"\n",
280+
"需要注意的一点是，这个问题的最终答案并不在最后一个单元格中！对于前面的背包问题，最终答案总是在最后的单元格中。\n",
281+
"\n",
282+
"但对于最长公共子串问题，答案为**网格中最大的数字**——它可能并不位于最后的单元格中。\n",
283+
"\n",
284+
"**具体实现代码如下：**\n",
285+
"\n",
286+
"可参考[GeeksforGeeks: Longest Common Substring | DP-29](https://www.geeksforgeeks.org/longest-common-substring-dp-29/)"
287+
]
288+
},
289+
{
290+
"cell_type": "code",
291+
"execution_count": 4,
292+
"metadata": {},
293+
"outputs": [
294+
{
295+
"data": {
296+
"text/plain": [
297+
"2"
298+
]
299+
},
300+
"execution_count": 4,
301+
"metadata": {},
302+
"output_type": "execute_result"
303+
}
304+
],
305+
"source": [
306+
"# Python3 implementation of Finding \n",
307+
"# Length of Longest Common Substring \n",
308+
"\n",
309+
"# Returns length of longest common \n",
310+
"# substring of s1[0..m-1] and s2[0..n-1] \n",
311+
"\n",
312+
"def LCSubStr(s1,s2):\n",
313+
" # 最长公共子串(Longest Common Substring)\n",
314+
" m = len(s1)\n",
315+
" n = len(s2)\n",
316+
" dp = [[0]*(n+1) for _ in range(m+1)] #初始化，添加一行、一列0 一共m+1行，n+1列\n",
317+
" result = 0 #保存最长公共字串的长度\n",
318+
" for i in range(1,m+1):\n",
319+
" for j in range(1,n+1):\n",
320+
" if s1[i-1] == s2[j-1]: # 相同\n",
321+
" dp[i][j] = dp[i-1][j-1]+1\n",
322+
" result = max(result, dp[i][j])\n",
323+
" else: # 不同\n",
324+
" dp[i][j] = 0\n",
325+
" return result\n",
326+
"\n",
327+
"s1 = [1,3,4,5,6,7,7,8]\n",
328+
"s2 = [3,5,7,4,8,6,7,8,2]\n",
329+
"LCSubStr(s1,s2)"
330+
]
331+
},
332+
{
333+
"cell_type": "markdown",
334+
"metadata": {},
335+
"source": [
336+
"## 9.4 最长公共子序列(Longest Common Subsequence，LCS)\n",
337+
"\n",
338+
"假设Alex不小心输入了fosh，他原本想输入的是fish还是fort呢？如果我们使用最长公共子串公式来比较它们：\n",
339+
"\n",
340+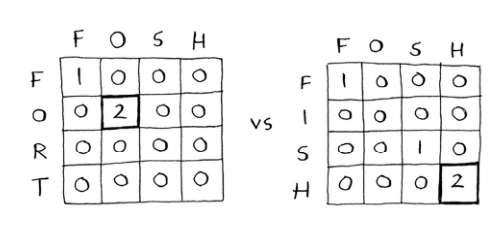
"![](https://raw.githubusercontent.com/hostimg/img/gh-pages/s/20190822193436.png)\n",
341+
"\n",
342+
"最长公共子串的长度相同，都包含两个字母！但fosh与fish更像。\n",
343+
"\n",
344+
"所以这里应该比较的是**最长公共子序列**：两个单词中**都有的序列**包含的**字母数**。\n",
345+
"\n",
346+
"**最长公共子序列（LCS,Longest Common Subsequence）**：它不要求所求得的字符在所给的字符串中是连续的,而**最长公共子串**则要求字符串是连续的。\n",
347+
"\n",
348+
"如何计算最长公共子序列呢？\n",
349+
"\n",
350+
"### 9.4.1 动态规划算法\n",
351+
"\n",
352+
"下面是填写各个单元格时使用的公式：\n",
353+
"\n",
354+
"![](https://raw.githubusercontent.com/hostimg/img/gh-pages/s/20190822194836.png)\n",
355+
"\n",
356+
"最终的网格如下：\n",
357+
"\n",
358+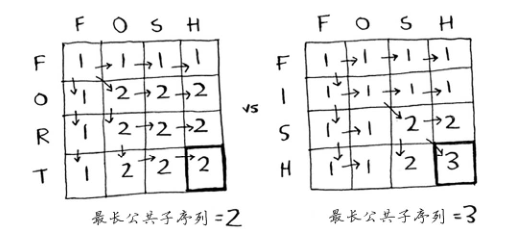
"![](https://raw.githubusercontent.com/hostimg/img/gh-pages/s/20190822194437.png)\n",
359+
"\n",
360+
"伪代码如下：\n",
361+
"\n",
362+
"```python\n",
363+
"if word_a[i] == word_b[j]:\n",
364+
" cell[i][j] = cell[i-1][j-1] + 1\n",
365+
"else:\n",
366+
" cell[i][j] = max(cell[i-1][j], cell[i][j-1])\n",
367+
"```"
368+
]
369+
},
370+
{
371+
"cell_type": "markdown",
372+
"metadata": {},
373+
"source": [
374+
"**具体实现代码如下：**\n",
375+
"\n",
376+
"可参考[GeeksforGeeks: Longest Common Subsequence | DP-4](https://www.geeksforgeeks.org/longest-common-subsequence-dp-4/)"
377+
]
378+
},
379+
{
380+
"cell_type": "code",
381+
"execution_count": 5,
382+
"metadata": {},
383+
"outputs": [
384+
{
385+
"name": "stdout",
386+
"output_type": "stream",
387+
"text": [
388+
"5\n"
389+
]
390+
},
391+
{
392+
"data": {
393+
"text/plain": [
394+
"[[0, 0, 0, 0, 0, 0, 0, 0, 0, 0],\n",
395+
" [0, 0, 0, 0, 0, 0, 0, 0, 0, 0],\n",
396+
" [0, 1, 1, 1, 1, 1, 1, 1, 1, 1],\n",
397+
" [0, 1, 1, 1, 2, 2, 2, 2, 2, 2],\n",
398+
" [0, 1, 2, 2, 2, 2, 2, 2, 2, 2],\n",
399+
" [0, 1, 2, 2, 2, 2, 3, 3, 3, 3],\n",
400+
" [0, 1, 2, 3, 3, 3, 3, 4, 4, 4],\n",
401+
" [0, 1, 2, 3, 3, 3, 3, 4, 4, 4],\n",
402+
" [0, 1, 2, 3, 3, 4, 4, 4, 5, 5]]"
403+
]
404+
},
405+
"execution_count": 5,
406+
"metadata": {},
407+
"output_type": "execute_result"
408+
}
409+
],
410+
"source": [
411+
"# Dynamic Programming implementation of LCS problem \n",
412+
"def LCS(s1,s2):\n",
413+
" # 最长公共子序列(Longest Common Subsequence)\n",
414+
" m = len(s1)\n",
415+
" n = len(s2)\n",
416+
" dp = [[0]*(n+1) for _ in range(m+1)] #初始化，添加一行、一列0 一共m+1行，n+1列\n",
417+
" result = 0 #保存最长公共字串的长度\n",
418+
" for i in range(1,m+1):\n",
419+
" for j in range(1,n+1):\n",
420+
" if s1[i-1] == s2[j-1]: # 相同\n",
421+
" dp[i][j] = dp[i-1][j-1]+1\n",
422+
" result = max(result, dp[i][j])\n",
423+
" else: # 不同\n",
424+
" dp[i][j] = max(dp[i-1][j],dp[i][j-1])\n",
425+
" return dp,result\n",
426+
"\n",
427+
"s1 = [1,3,4,5,6,7,7,8]\n",
428+
"s2 = [3,5,7,4,8,6,7,8,2]\n",
429+
"dp,result = LCS(s1,s2)\n",
430+
"print(result)\n",
431+
"dp"
432+
]
433+
},
434+
{
435+
"cell_type": "markdown",
436+
"metadata": {},
437+
"source": [
438+
"### 9.4.2 递归算法\n",
439+
"\n",
440+
"考虑两个字符串的最后一个字符：\n",
441+
"\n",
442+
"- 1.如果最后一个字符相同，可以转化为均去掉最后一个字符之后的LCS，在加上1\n",
443+
"- 2.如果最后一个字符不同，可以转化为：s1去掉最后一个字符和s2的LCS，以及s2去掉最后一个字符和s1的LCS，两者取大值。如：\n",
444+
"\n",
445+
"`LCS(“ABCDGH”, “AEDFHR”) = MAX ( LCS(“ABCDG”, “AEDFHR”), LCS(“ABCDGH”, “AEDFH”) )`\n",
446+
"\n",
447+
"上述朴素递归方法的时间复杂度在最坏情况下为$O(2^n)$ ，当X和Y的所有字符不匹配时，即LCS的长度为0时，发生最坏情况。\n",
448+
"\n",
449+
"**具体代码如下：**"
450+
]
451+
},
452+
{
453+
"cell_type": "code",
454+
"execution_count": 6,
455+
"metadata": {},
456+
"outputs": [
457+
{
458+
"name": "stdout",
459+
"output_type": "stream",
460+
"text": [
461+
"Length of LCS is 4\n"
462+
]
463+
}
464+
],
465+
"source": [
466+
"# A Naive recursive Python implementation of LCS problem \n",
467+
" \n",
468+
"def LCS(X, Y, m, n): \n",
469+
" if m == 0 or n == 0: \n",
470+
" return 0\n",
471+
" elif X[m-1] == Y[n-1]: \n",
472+
" return 1 + LCS(X, Y, m-1, n-1)\n",
473+
" else: \n",
474+
" return max(LCS(X, Y, m, n-1), LCS(X, Y, m-1, n))\n",
475+
" \n",
476+
" \n",
477+
"# Driver program to test the above function \n",
478+
"X = \"AGGTAB\"\n",
479+
"Y = \"GXTXAYB\"\n",
480+
"print(\"Length of LCS is \", LCS(X , Y, len(X), len(Y))) "
481+
]
482+
},
483+
{
484+
"cell_type": "markdown",
485+
"metadata": {},
486+
"source": [
487+
"**动态规划的实际应用**：\n",
488+
"\n",
489+
"- 生物学家根据最长公共序列来确定DNA链的相似性，进而判断度两种动物或疾病有多相似。最长公共序列还被用来寻找多发性硬化症治疗方案。\n",
490+
"- 你使用过诸如 git diff 等命令吗？它们指出两个文件的差异，也是使用动态规划实现的。\n",
491+
"- 前面讨论了字符串的相似程度。编辑距离（levenshtein distance）指出了两个字符串的相似程度，也是使用动态规划计算得到的。编辑距离算法的用途很多，从拼写检查到判断用户上传的资料是否是盗版，都在其中。\n",
492+
"- 你使用过诸如Microsoft Word等具有断字功能的应用程序吗？它们如何确定在什么地方断字以确保行长一致呢？使用动态规划！"
493+
]
494+
},
495+
{
496+
"cell_type": "markdown",
497+
"metadata": {},
498+
"source": [
499+
"## 9.5 小结\n",
500+
"\n",
501+
"- 需要在给定约束条件下优化某种指标时，动态规划很有用。\n",
502+
"- 问题可分解为离散子问题时，可使用动态规划来解决。\n",
503+
"- 每种动态规划解决方案都涉及网格。\n",
504+
"- 单元格中的值通常就是你要优化的值。\n",
505+
"- 每个单元格都是一个子问题，因此你需要考虑如何将问题分解为子问题。\n",
506+
"- 没有放之四海皆准的计算动态规划解决方案的公式。"
507+
]
229508
}
230509
],
231510
"metadata": {
232511
"kernelspec": {
233-
"display_name": "Python 3 (system-wide)",
512+
"display_name": "Python 3",
234513
"language": "python",
235514
"name": "python3"
236515
},

0 commit comments

Comments
 (0)