|
4 | 4 | "cell_type": "markdown", |
5 | 5 | "metadata": {}, |
6 | 6 | "source": [ |
7 | | - "字符串匹配的KMP算法\n", |
| 7 | + "# 字符串匹配——KMP算法\n", |
8 | 8 | "\n", |
9 | | - "http://www.ruanyifeng.com/blog/2013/05/Knuth%E2%80%93Morris%E2%80%93Pratt_algorithm.html" |
| 9 | + "[字符串匹配的KMP算法-阮一峰](http://www.ruanyifeng.com/blog/2013/05/Knuth%E2%80%93Morris%E2%80%93Pratt_algorithm.html)\n", |
| 10 | + "\n", |
| 11 | + "[从头到尾彻底理解KMP(2014年8月22日版)-July](https://blog.csdn.net/v_july_v/article/details/7041827)\n", |
| 12 | + "\n", |
| 13 | + "有一个字符串\"BBC ABCDAB ABCDABCDABDE\",我想知道,里面是否包含另一个字符串\"ABCDABD\"?\n", |
| 14 | + "\n", |
| 15 | + "## 1.暴力匹配方法Brute Force(BF)算法:\n", |
| 16 | + "\n", |
| 17 | + " 如果用暴力匹配的思路,并假设现在文本串S匹配到 i 位置,模式串P匹配到 j 位置,则有:\n", |
| 18 | + "\n", |
| 19 | + "如果当前字符匹配成功(即S[i] == P[j]),则i++,j++,继续匹配下一个字符;\n", |
| 20 | + "\n", |
| 21 | + "如果失配(即S[i]! = P[j]),令i = i - (j - 1),j = 0。相当于每次匹配失败时,i 回溯并向前移动一位,j 被置为0。\n", |
| 22 | + "\n", |
| 23 | + "代码:" |
| 24 | + ] |
| 25 | + }, |
| 26 | + { |
| 27 | + "cell_type": "code", |
| 28 | + "execution_count": 1, |
| 29 | + "metadata": {}, |
| 30 | + "outputs": [ |
| 31 | + { |
| 32 | + "data": { |
| 33 | + "text/plain": [ |
| 34 | + "4" |
| 35 | + ] |
| 36 | + }, |
| 37 | + "execution_count": 1, |
| 38 | + "metadata": {}, |
| 39 | + "output_type": "execute_result" |
| 40 | + } |
| 41 | + ], |
| 42 | + "source": [ |
| 43 | + "def BFAlgo(s,p):\n", |
| 44 | + " slen = len(s)\n", |
| 45 | + " plen = len(p)\n", |
| 46 | + " i = j = 0\n", |
| 47 | + " while i < slen and j < plen:\n", |
| 48 | + " if s[i] == p[j]: #匹配到则继续往下匹配\n", |
| 49 | + " i += 1\n", |
| 50 | + " j += 1 #i=slen或者j=plen时退出while循环\n", |
| 51 | + " else: # 不匹配则回溯\n", |
| 52 | + " i = i - j + 1\n", |
| 53 | + " j = 0\n", |
| 54 | + " if j == plen:\n", |
| 55 | + " return i - j\n", |
| 56 | + " else:\n", |
| 57 | + " return -1\n", |
| 58 | + "\n", |
| 59 | + "s = \"abbaabbaaba\"\n", |
| 60 | + "p = \"abbaaba\"\n", |
| 61 | + "BFAlgo(s,p)" |
| 62 | + ] |
| 63 | + }, |
| 64 | + { |
| 65 | + "cell_type": "markdown", |
| 66 | + "metadata": {}, |
| 67 | + "source": [ |
| 68 | + "## 2.KMP算法\n", |
| 69 | + "\n", |
| 70 | + "### [字符串匹配的KMP算法-阮一峰](http://www.ruanyifeng.com/blog/2013/05/Knuth%E2%80%93Morris%E2%80%93Pratt_algorithm.html)\n", |
| 71 | + "\n", |
| 72 | + "#### 1.部分匹配表\n", |
| 73 | + "\n", |
| 74 | + "针对搜索词,算出一张《部分匹配表》(Partial Match Table),LPS(longest prefix suffix) 最长前缀后缀公共元素长度\n", |
| 75 | + "\n", |
| 76 | + "\n", |
| 77 | + "\n", |
| 78 | + "\n", |
| 79 | + "\"部分匹配值\"就是\"前缀\"和\"后缀\"的最长的共有元素的长度。以\"ABCDABD\"为例,\n", |
| 80 | + "\n", |
| 81 | + "\n", |
| 82 | + "- \"A\"的前缀和后缀都为空集,共有元素的长度为0;\n", |
| 83 | + "\n", |
| 84 | + "- \"AB\"的前缀为[A],后缀为[B],共有元素的长度为0;\n", |
| 85 | + "\n", |
| 86 | + "- \"ABC\"的前缀为[A, AB],后缀为[BC, C],共有元素的长度0;\n", |
| 87 | + "\n", |
| 88 | + "- \"ABCD\"的前缀为[A, AB, ABC],后缀为[BCD, CD, D],共有元素的长度为0;\n", |
| 89 | + "\n", |
| 90 | + "- \"ABCDA\"的前缀为[A, AB, ABC, ABCD],后缀为[BCDA, CDA, DA, A],共有元素为\"A\",长度为1;\n", |
| 91 | + "\n", |
| 92 | + "- \"ABCDAB\"的前缀为[A, AB, ABC, ABCD, ABCDA],后缀为[BCDAB, CDAB, DAB, AB, B],共有元素为\"AB\",长度为2;\n", |
| 93 | + "\n", |
| 94 | + "- \"ABCDABD\"的前缀为[A, AB, ABC, ABCD, ABCDA, ABCDAB],后缀为[BCDABD, CDABD, DABD, ABD, BD, D],共有元素的长度为0。\n", |
| 95 | + "\n", |
| 96 | + "#### 2.匹配,移动\n", |
| 97 | + "\n", |
| 98 | + "先找到和待匹配字符串第一位相同的字符,一直匹配到第一个不匹配的字符。\n", |
| 99 | + "\n", |
| 100 | + "\n", |
| 101 | + "\n", |
| 102 | + "已知空格与D不匹配时,前面六个字符\"ABCDAB\"是匹配的。查表可知,最后一个匹配字符B对应的\"部分匹配值\"为2,因此按照下面的公式算出向后移动的位数:\n", |
| 103 | + "\n", |
| 104 | + "```\n", |
| 105 | + "移动位数 = 已匹配的字符数 - 对应的部分匹配值\n", |
| 106 | + "```\n", |
| 107 | + "\n", |
| 108 | + "因为 6 - 2 等于4,所以将搜索词向后移动4位。\n", |
| 109 | + "\n", |
| 110 | + "\n", |
| 111 | + "\n", |
| 112 | + "可以看出,p串最前面的两个AB移动到了对应于s串的AB的位置。" |
| 113 | + ] |
| 114 | + }, |
| 115 | + { |
| 116 | + "cell_type": "markdown", |
| 117 | + "metadata": {}, |
| 118 | + "source": [ |
| 119 | + "### [从头到尾彻底理解KMP(2014年8月22日版)-July](https://blog.csdn.net/v_july_v/article/details/7041827)\n", |
| 120 | + "\n", |
| 121 | + "假设现在文本串S匹配到 i 位置,模式串P匹配到 j 位置\n", |
| 122 | + "\n", |
| 123 | + "- 如果j = -1,或者当前字符匹配成功(即S[i] == P[j]),都令i++,j++,继续匹配下一个字符;\n", |
| 124 | + "- 如果j != -1,且当前字符匹配失败(即S[i] != P[j]),则令 i 不变,j = next[j]。此举意味着失配时,模式串P相对于文本串S向右移动了j - next [j] 位。\n", |
| 125 | + " - 换言之,当匹配失败时,模式串向右移动的位数为:失配字符所在位置 - 失配字符对应的next 值(next 数组的求解会在下文的3.3.3节中详细阐述),即移动的实际位数为:j - next[j],且此值大于等于1。\n", |
| 126 | + " \n", |
| 127 | + "很快,你也会意识到next 数组各值的含义:代表当前字符之前的字符串中,有多大长度的相同前缀后缀。例如如果next [j] = k,代表j 之前的字符串中有最大长度为k 的相同前缀后缀。\n", |
| 128 | + "\n", |
| 129 | + "此也意味着在某个字符失配时,该字符对应的next 值会告诉你下一步匹配中,模式串应该跳到哪个位置(跳到next [j] 的位置)。如果next [j] 等于0或-1,则跳到模式串的开头字符,若next [j] = k 且 k > 0,代表下次匹配跳到j 之前的某个字符,而不是跳到开头,且具体跳过了k 个字符。\n", |
| 130 | + "\n", |
| 131 | + "转换成代码表示(nextArr求解见下文):" |
| 132 | + ] |
| 133 | + }, |
| 134 | + { |
| 135 | + "cell_type": "code", |
| 136 | + "execution_count": 2, |
| 137 | + "metadata": {}, |
| 138 | + "outputs": [], |
| 139 | + "source": [ |
| 140 | + "def KMPAlgo(s,p):\n", |
| 141 | + " i=j=0\n", |
| 142 | + " slen = len(s)\n", |
| 143 | + " plen = len(p)\n", |
| 144 | + " while i < slen and j < plen:\n", |
| 145 | + " #如果j = -1,或者当前字符匹配成功(即S[i] == P[j]),都令i++,j++ \n", |
| 146 | + " if j==-1 or s[i] == s[j]:\n", |
| 147 | + " i += 1\n", |
| 148 | + " j += 1\n", |
| 149 | + " #如果j != -1,且当前字符匹配失败(即S[i] != P[j]),则令 i 不变,j = next[j]\n", |
| 150 | + " else:\n", |
| 151 | + " j = nextArr[j] #nextArr[j]即为j所对应的next值\n", |
| 152 | + " if j == plen:\n", |
| 153 | + " return i - j\n", |
| 154 | + " else:\n", |
| 155 | + " return -1" |
| 156 | + ] |
| 157 | + }, |
| 158 | + { |
| 159 | + "cell_type": "markdown", |
| 160 | + "metadata": {}, |
| 161 | + "source": [ |
| 162 | + "**步骤:**\n", |
| 163 | + "\n", |
| 164 | + "#### 1.寻找前缀后缀最长公共元素长度\n", |
| 165 | + "\n", |
| 166 | + "如abab为0,0,1,2\n", |
| 167 | + "\n", |
| 168 | + "#### 2.求next数组\n", |
| 169 | + "\n", |
| 170 | + "next 数组考虑的是除当前字符外的最长相同前缀后缀,所以通过第1步骤求得各个前缀后缀的公共元素的最大长度后,只要稍作变形即可:将第1步骤中求得的值整体右移一位,然后初值赋为-1,如下表格所示:\n", |
| 171 | + "\n", |
| 172 | + "-1,0,0,1\n", |
| 173 | + "\n", |
| 174 | + "如对于aba来说,第3个字符a之前的字符串ab中有长度为0的相同前缀后缀,所以第3个字符a对应的next值为0;\n", |
| 175 | + "\n", |
| 176 | + "而对于abab来说,第4个字符b之前的字符串aba中有长度为1的相同前缀后缀a,所以第4个字符b对应的next值为1。\n", |
| 177 | + "\n", |
| 178 | + "#### 3.根据next数组进行匹配\n", |
| 179 | + "\n", |
| 180 | + "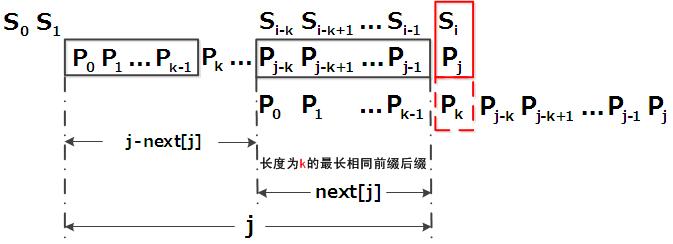\n", |
| 181 | + "\n", |
| 182 | + " 综上,KMP的next 数组相当于告诉我们:当模式串中的某个字符跟文本串中的某个字符匹配失配时,模式串下一步应该跳到哪个位置。如模式串中在j 处的字符跟文本串在i 处的字符匹配失配时,下一步用next [j] 处的字符继续跟文本串i 处的字符匹配,相当于模式串向右移动 j - next[j] 位。" |
| 183 | + ] |
| 184 | + }, |
| 185 | + { |
| 186 | + "cell_type": "code", |
| 187 | + "execution_count": 3, |
| 188 | + "metadata": {}, |
| 189 | + "outputs": [ |
| 190 | + { |
| 191 | + "data": { |
| 192 | + "text/plain": [ |
| 193 | + "[-1, 0, 0, 1, 2]" |
| 194 | + ] |
| 195 | + }, |
| 196 | + "execution_count": 3, |
| 197 | + "metadata": {}, |
| 198 | + "output_type": "execute_result" |
| 199 | + } |
| 200 | + ], |
| 201 | + "source": [ |
| 202 | + "# next数组计算\n", |
| 203 | + "def getNext(p):\n", |
| 204 | + " plen = len(p)\n", |
| 205 | + " nextArr = [0]*plen\n", |
| 206 | + " nextArr[0] = -1\n", |
| 207 | + " k = -1\n", |
| 208 | + " j = 0\n", |
| 209 | + " while j < plen-1: # p[k]表示前缀,p[j]表示后缀\n", |
| 210 | + " if k == -1 or p[j] == p[k]:\n", |
| 211 | + " k += 1\n", |
| 212 | + " j += 1\n", |
| 213 | + " nextArr[j] = k\n", |
| 214 | + " else:\n", |
| 215 | + " k = nextArr[k]\n", |
| 216 | + " return nextArr\n", |
| 217 | + "\n", |
| 218 | + "getNext(\"ababb\")" |
| 219 | + ] |
| 220 | + }, |
| 221 | + { |
| 222 | + "cell_type": "markdown", |
| 223 | + "metadata": {}, |
| 224 | + "source": [ |
| 225 | + "#### 4.Next 数组的优化\n", |
| 226 | + "\n", |
| 227 | + " 行文至此,咱们全面了解了暴力匹配的思路、KMP算法的原理、流程、流程之间的内在逻辑联系,以及next 数组的简单求解(《最大长度表》整体右移一位,然后初值赋为-1)和代码求解,最后基于《next 数组》的匹配,看似洋洋洒洒,清晰透彻,但以上忽略了一个小问题。\n", |
| 228 | + "\n", |
| 229 | + " 比如,如果用之前的next 数组方法求模式串“abab”的next 数组,可得其next 数组为-1 0 0 1(0 0 1 2整体右移一位,初值赋为-1),当它跟下图中的文本串去匹配的时候,发现b跟c失配,于是模式串右移j - next[j] = 3 - 1 =2位。\n", |
| 230 | + "\n", |
| 231 | + "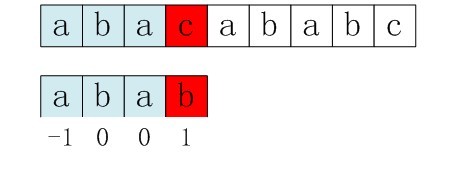\n", |
| 232 | + "\n", |
| 233 | + "右移2位后,b又跟c失配。事实上,因为在上一步的匹配中,已经得知p[3] = b,与s[3] = c失配,而右移两位之后,让p[ next[3] ] = p[1] = b 再跟s[3]匹配时,必然失配。问题出在哪呢?\n", |
| 234 | + "\n", |
| 235 | + "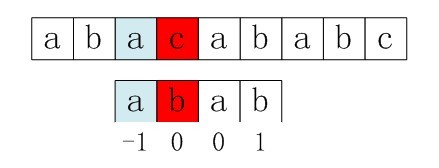\n", |
| 236 | + "\n", |
| 237 | + "问题出在不该出现p[j] = p[ next[j] ]。为什么呢?理由是:当p[j] != s[i] 时,下次匹配必然是p[ next [j]] 跟s[i]匹配,如果p[j] = p[ next[j] ],必然导致后一步匹配失败(因为p[j]已经跟s[i]失配,然后你还用跟p[j]等同的值p[next[j]]去跟s[i]匹配,很显然,必然失配),所以不能允许p[j] = p[ next[j ]]。如果出现了p[j] = p[ next[j] ]咋办呢?如果出现了,则需要再次递归,即令next[j] = next[ next[j] ]。\n", |
| 238 | + "\n", |
| 239 | + "所以,咱们得修改下求next 数组的代码。\n" |
| 240 | + ] |
| 241 | + }, |
| 242 | + { |
| 243 | + "cell_type": "code", |
| 244 | + "execution_count": 4, |
| 245 | + "metadata": {}, |
| 246 | + "outputs": [ |
| 247 | + { |
| 248 | + "data": { |
| 249 | + "text/plain": [ |
| 250 | + "[-1, 0, -1, 0, 2, -1, 0, -1, 0]" |
| 251 | + ] |
| 252 | + }, |
| 253 | + "execution_count": 4, |
| 254 | + "metadata": {}, |
| 255 | + "output_type": "execute_result" |
| 256 | + } |
| 257 | + ], |
| 258 | + "source": [ |
| 259 | + "# 优化过后的next 数组求法\n", |
| 260 | + "def getNext(p):\n", |
| 261 | + " plen = len(p)\n", |
| 262 | + " nextArr = [0]*plen\n", |
| 263 | + " nextArr[0] = -1\n", |
| 264 | + " k = -1\n", |
| 265 | + " j = 0\n", |
| 266 | + " while j < plen-1: # p[k]表示前缀,p[j]表示后缀\n", |
| 267 | + " if k == -1 or p[j] == p[k]:\n", |
| 268 | + " k += 1\n", |
| 269 | + " j += 1\n", |
| 270 | + " #较之前next数组求法,改动在下面4行\n", |
| 271 | + " if p[j] != p[k]:\n", |
| 272 | + " nextArr[j] = k\n", |
| 273 | + " else:\n", |
| 274 | + " #因为不能出现p[j] = p[ next[j ]],所以当出现时需要继续递归,k = next[k] = next[next[k]]\n", |
| 275 | + " nextArr[j] = nextArr[k]\n", |
| 276 | + " else:\n", |
| 277 | + " k = nextArr[k]\n", |
| 278 | + " return nextArr\n", |
| 279 | + "\n", |
| 280 | + "getNext(\"ababcabab\")" |
| 281 | + ] |
| 282 | + }, |
| 283 | + { |
| 284 | + "cell_type": "markdown", |
| 285 | + "metadata": {}, |
| 286 | + "source": [ |
| 287 | + "对于优化后的next数组可以发现一点:如果模式串的后缀跟前缀相同,那么它们的next值也是相同的,例如模式串abcabc,它的前缀后缀都是abc,其优化后的next数组为:-1 0 0 -1 0 0,前缀后缀abc的next值都为-1 0 0。" |
| 288 | + ] |
| 289 | + }, |
| 290 | + { |
| 291 | + "cell_type": "markdown", |
| 292 | + "metadata": {}, |
| 293 | + "source": [ |
| 294 | + "## 3.KMP算法完整代码" |
| 295 | + ] |
| 296 | + }, |
| 297 | + { |
| 298 | + "cell_type": "code", |
| 299 | + "execution_count": 5, |
| 300 | + "metadata": {}, |
| 301 | + "outputs": [ |
| 302 | + { |
| 303 | + "name": "stdout", |
| 304 | + "output_type": "stream", |
| 305 | + "text": [ |
| 306 | + "15\n" |
| 307 | + ] |
| 308 | + } |
| 309 | + ], |
| 310 | + "source": [ |
| 311 | + "# 优化过后的next 数组求法\n", |
| 312 | + "def getNext(p):\n", |
| 313 | + " plen = len(p)\n", |
| 314 | + " nextArr = [0]*plen\n", |
| 315 | + " nextArr[0] = -1\n", |
| 316 | + " k = -1\n", |
| 317 | + " j = 0\n", |
| 318 | + " while j < plen-1: # p[k]表示前缀,p[j]表示后缀\n", |
| 319 | + " if k == -1 or p[j] == p[k]:\n", |
| 320 | + " k += 1\n", |
| 321 | + " j += 1\n", |
| 322 | + " #较之前next数组求法,改动在下面4行\n", |
| 323 | + " if p[j] != p[k]:\n", |
| 324 | + " nextArr[j] = k\n", |
| 325 | + " else:\n", |
| 326 | + " #因为不能出现p[j] = p[ next[j ]],所以当出现时需要继续递归,k = next[k] = next[next[k]]\n", |
| 327 | + " nextArr[j] = nextArr[k]\n", |
| 328 | + " else:\n", |
| 329 | + " k = nextArr[k]\n", |
| 330 | + " return nextArr\n", |
| 331 | + "\n", |
| 332 | + "def KMPAlgo(s,p):\n", |
| 333 | + " #KMP算法\n", |
| 334 | + " i = j = 0\n", |
| 335 | + " slen = len(s)\n", |
| 336 | + " plen = len(p)\n", |
| 337 | + " nextArr = getNext(p)\n", |
| 338 | + " while i < slen and j < plen:\n", |
| 339 | + " #如果j = -1,或者当前字符匹配成功(即S[i] == P[j]),都令i++,j++ \n", |
| 340 | + " if j==-1 or s[i] == p[j]:\n", |
| 341 | + " i += 1\n", |
| 342 | + " j += 1\n", |
| 343 | + " #如果j != -1,且当前字符匹配失败(即S[i] != P[j]),则令 i 不变,j = next[j]\n", |
| 344 | + " else:\n", |
| 345 | + " j = nextArr[j] #nextArr[j]即为j所对应的next值\n", |
| 346 | + " if j == plen:\n", |
| 347 | + " return i - j\n", |
| 348 | + " else:\n", |
| 349 | + " return -1\n", |
| 350 | + "\n", |
| 351 | + "if __name__==\"__main__\":\n", |
| 352 | + " s = \"BBC ABCDAB ABCDABCDABDE\"\n", |
| 353 | + " p = \"ABCDABD\"\n", |
| 354 | + " print(KMPAlgo(s,p))" |
10 | 355 | ] |
11 | 356 | } |
12 | 357 | ], |
13 | 358 | "metadata": { |
14 | 359 | "kernelspec": { |
15 | | - "display_name": "tf36", |
| 360 | + "display_name": "Python 3", |
16 | 361 | "language": "python", |
17 | | - "name": "tf36" |
| 362 | + "name": "python3" |
18 | 363 | }, |
19 | 364 | "language_info": { |
20 | 365 | "codemirror_mode": { |
|
26 | 371 | "name": "python", |
27 | 372 | "nbconvert_exporter": "python", |
28 | 373 | "pygments_lexer": "ipython3", |
29 | | - "version": "3.6.8" |
| 374 | + "version": "3.7.3" |
30 | 375 | } |
31 | 376 | }, |
32 | 377 | "nbformat": 4, |
|
0 commit comments